Котангенс — тригонометрическая функция и одно из ключевых понятий тригонометрии. В этом разделе математики изучают практическое применение этой и подобных, связанных с ней функций в геометрии.
Общее понятие
Без тригонометрических вычислений не обходится ни одна наука, связанная с вычислением углов. Они широко используются не только в геометрии, но и в инженерном деле, физике, различных технических дисциплинах. Особенно важен данный раздел для астрономии и географии, навигационных систем.
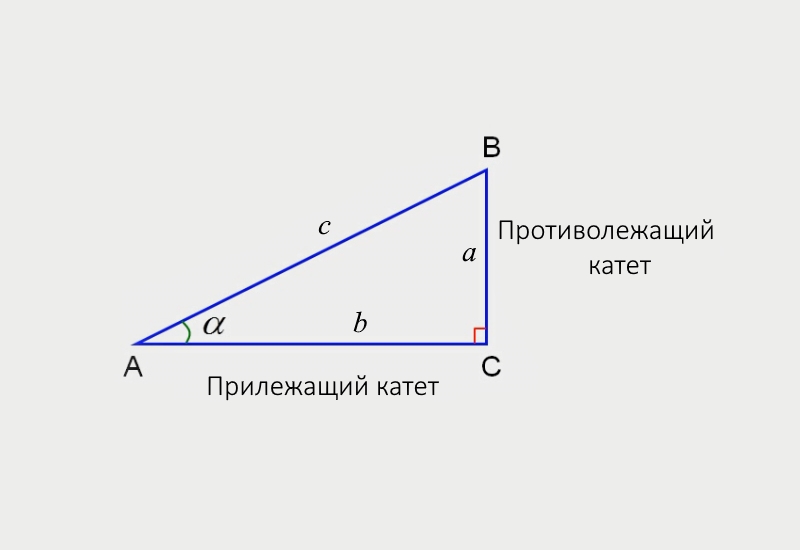
Котангенсом угла называют величину, обратно пропорциональную другой тангенсу, он определяется как отношение прилежащего катета к противолежащему.
Некоторым проще запомнить эту функцию в таком виде: отношение ближайшего от угла катета к удалённому.
В данном случае: ctgα= b/a.
Связь с другими функциями и свойства
Тангенсом острого угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему.
Есть у tg и ctg связь с двумя основополагающими функциями тригонометрии — синусом и косинусом:
- tg α= sinα/cosα;
- ctgα= cosα/sinα.
Благодаря существующим тригонометрическим формулам, в которых задействованы вышеназванные функции, удаётся решать самые разные задачи из курса тригонометрии.
График функции y=ctgx для для всех x из области допустимых значений выглядит так:
Свойства функции y = ctg x:
- нечётная;
- убывает в интервале от 0 до π (Пи);
- область определения — от 0 до π, кроме точек 0 и π;
- множество значений — на всей числовой прямой;
- периодическая, период равен числу π;
- график симметричен относительно начала координат;
- убывает на каждом интервале области определения;
- нет экстремумов;
- непрерывная на каждом интервале области определения;
- график не ограничен снизу и сверху.
Значения котангенсов углов от 0 до 360 градусов подсчитаны и сведены в таблицу. Её обычно используют, если под рукой нет калькулятора.